(After Basson 2000)
Introduction
GPR is an electromagnetic (EM) geophysical method for high-resolution detection, imaging and mapping of subsurface soils and rock conditions. The idea of using the propagation of high-frequency EM waves for subsurface investigations can be traced back to the beginning of the century, but the earliest references to the possibility of using sharp EM pulses appear in German patents from the 1920’s. Radar (short for radio detection and ranging), a system that uses short EM pulses, was fully developed in Britain for defense against enemy planes during the Second World War, although several such systems did exist in Britain, France, Germany and the USA before the War.
In addition to its numerous military and civil applications, radar is now a very important tool in ground investigations, normally from the near surface to a depth of several tens of meters. During more than two decades of development, GPR systems have become the geophysical tools that provide the subsurface window for a variety of geological, engineering, environmental and archaeological applications: determining the thicknesses of soil horizons and depth to water table; detecting air-filled subsurface cavities, buried channels and tunnels; mapping contamination plumes; investigating the condition of dam cores, masonry structures and bridge piers; detecting buried objects in archeological surveys; finding ice or permafrost thicknesses; studying the condition of the asphalt layer on roads, etc.
Fundamentals of GPR
A typical GPR system has three main components: Transmitter and receiver that are directly connected to an antenna, and a control unit (timing) (Fig. 1). The transmitting antenna radiates a short high-frequency EM pulse into the ground, where it is refracted, diffracted and reflected primarily as it encounters changes in dielectric permittivity and electric conductivity.
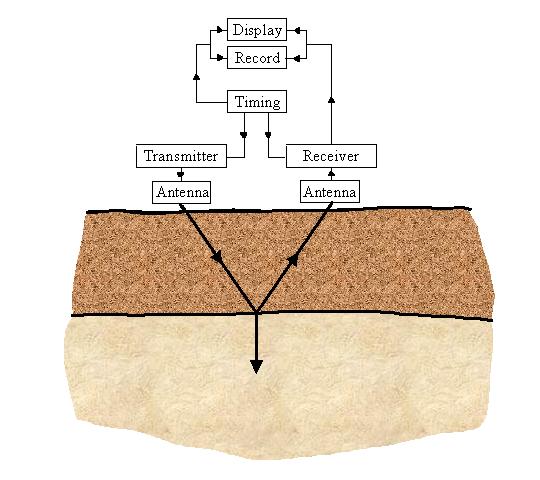
Figure 1: Flow chart for a typical GPR system [after Davis et al., 1989].
The propagation of a radar signal depends mainly on the electrical properties of the subsurface materials (see AppendixA for the electrical properties of geological media). Waves that are scattered back toward the earth’s surface induce a signal in the receiving antenna, and are recorded as digitized signals for display and further analysis (Fig. 2).
Figure 2: Comparison of actual and GPR-imaged subsurface profiles, demonstrating the capabilities of the GPR system as an imaging tool of the shallow subsurface. The cliff shown is in the site of Nesher Ramle quarry. Horizontal scales indicate positions of measurement stations along mapped profile; vertical scale indicates depth to the reflectors.
Figure 2a: Photograph of mapped quarry cliff showing complex structure in chalky-limestone layers. Area imaged by GPR is shown inside the dashed frame.
Figure 2b: Plot image display of black-filled wiggle traces (variable area, VAR).
Figure 2c: Variable-intensity plot image, displayed in grey levels. Note that most of the signals in the profiles are reflections exceptfor the two topmost events, which are two direct waves from the transmitter to the receiver, one in the air and the other one in the ground. The amplitude of these two topmost events is considerably strong: they generally appear as two thick reflections that reduce our ability to visualize the shallowest part of the profile.
The most common operation mode of GPR is the Reflection mode, whereby traces of returned waves are collected either continuously or in stations along a line, thus creating a time cross-section or a profile image of the subsurface. CMP (common mid point), or WARR (wide-angle reflection-refraction) sounding and Transillumination are other modes of operation.
Several types of radar such as frequency-modulated sine-wave radar or holographic radar are in use, but for ground investigations, the most commonly used (i.e. GPR) is the pulse radar. The development of these systems started around middle 1950’s and accelerated considerably after 1970 as a result of the tremendous progress that took place in electronics and computer technology. The principles of GPR and the landmarks in its development are discussed at length in Morey [1974], Annan and Davis [1977], Ulriksen [1982], Davis and Annan [1986, 1989], Basson [1992], Cook [1995] Parasnis [1997] and Basson [2000].
Display
GPR data are displayed on printer paper or on a computer screen during acquisition (i.e., during real time). For a given transect, the data consist of a cross-section of signal amplitudes (intensities) versus location (along the two-way time axis and the horizontal axis). The intensity values are digitally recorded for each trace separately, converted back into analogue signals and displayed as signal voltage amplitude versus two-way time (the RAMAC GPR system uses a 16 bit A/D converter to convert the recorded signal to 65,536 levels of amplitudes). The plot is referred to as a normal-incidence time section (when the transmitter-receiver offset is negligible relative to the investigated depth and at a monostatic configuration). Simple processing is generally needed for a conventional display; otherwise, the display may become illegible. Such a typical processing is the running average of three to five samples along each trace plus the average of three traces along the profile in order to increase the signal to noise ratio. Amplifying gainis neededto increase the visibility of the deeper parts of the image. Basic processing routines can be applied during operation in the field while the image is built, in a way that does not affect the collected data.
Two common display types of a GPR profile are shown in Figure 2. The profile, which was conducted at the Nesher-Ramle Quarry of the Cement Corporation of Israel (about 20 km southeast of Tel Aviv), images a sequence of folded and faulted chalky-limestone layers on the western margins of the Judea anticline. The data were collected using a RAMAC GPR system (see APPENDIX B for the description of the system). Figure2a shows the cliff along which the profile was conducted, part of the graded cliff that surrounds the open quarry. The GPR profile was conducted along 75 m on the middle step, 5-10 m from its edge, to cover the complex geological structure shown inside the dashed frame of the picture. The photograph and the profiles are compared in Figure 2, convincingly demonstrating the capability of GPR as an imaging tool in complex geological environments.
Contiguous wiggle trace curves, generally with a black fill of the positive (or the negative) area, are one common display type of the amplitudes intensity field (Fig. 2b). This type of plot is also known in seismic reflection as variable area (VAR). Another common display technique is the variable-intensity in which the intensity value-samples are represented by grey tones or by colors. Figure 2c is an example of a variable-intensity display in grey levels. In special cases, a combination of these methods can be useful.
Interpretation
Modern GPR and SR processing make the profiles look so much like cross-sections trough the earth, that it is tempting to interpret them as such. In some ways, this is a useful way of thinking because it drives the development of acquisition sensors and processing methods forward to this goal. However, excluding simple and normal cases, GPR sections are not simple slices through the earth. This is mainly because of the nature of propagation and interaction of the EM wave inside and outside the ground, and its sensitivity to reflecting interfaces and objects, which are not necessarily the same interfaces and objects that would be visible to the eyes. Yet, a proper interpretation of a GPR profile should be based on the comprehensive understanding of geological and environmental conditions.
An example of an interpretation is shown in Figure 3. Figure 3a shows the prominent stratigraphy, structures and faults on the photograph of the cliff: dipping folded layers, a syncline and several faults. Figure 2.3b shows the interpretation of those elements on the GPR profile.
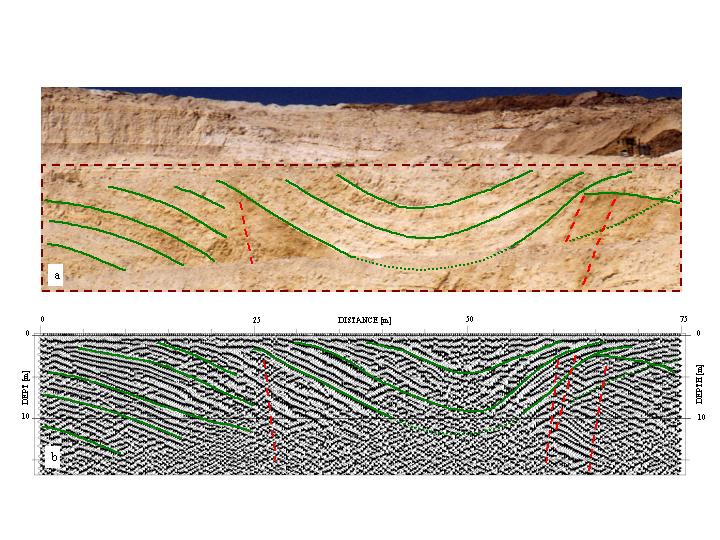
Figure 3: Interpretation of a GPR profile image.
Figure 3a: Interpretation of the prominent stratigraphic units, structures and faults distinguished on a photograph of the cliff in the Nesher Ramle quarry, including dipping folded layers, a syncline and several faults.
Figure 3b: The interpretation of those elements on the GPR profile.
Terms and Concepts of GPR
Antenna, pulse-width, center frequency and sampling
Most of the GPR systems use dipole antennas, either in monostatic or bistatic arrangement (monostaticwhen the same antenna is use for transmission and reception, and bistatic when two separate antennas are used). The length of the dipole antenna controls the character of the transmitted pulse, mainly the pulse width (duration), dt, so that a broader pulse requires a longer antenna. In practice, an antenna length of 1 m is required for a 10 ns pulse – the efficient GPR transmission duration – while pulses of 1-2 ns widths require antennas of 0.15-0.40 m long.
Normally, a GPR antenna emits a succession of pulses of the same form and duration at definite intervals. The frequency around which most of the pulses’ energy is concentrated is called the center frequency, fc. GPR systems are generally planned to create a frequency bandwidth, df (the pulse width at the frequency domain), which is similar to the center frequency, i.e., df ~ fc. In the time interval between two successive pulses, the receiving antenna measures the electric field in the incoming reflected puas an analogue signal, which is later amplified and converted to digital form. The interval at which the incoming signals are sampled is called sampling interval (its inverse is termed sampling frequency,fs).
The Sampling Theorem deals with the aspects of signal sampling [Yilmaz, 1987; Dobrin and Savit, 1988]. The criterion of the Sampling Theorem, for a faithful pulse represented by its samples, is that the sampling frequency must be at least twice as high as the maximum frequency fmaxof the pulse, i.e.:
(1) fs > 2fmax
Operation modes and stacking
Most surface investigations with GPR, whether they use continuous profiling or stationary point collection methods, are made in reflection mode. Both methods are usually applied using a cross-line antenna configuration in which dipoles are fitted perpendicular to the profile direction. In continuous profiling, the antennas are pulled along the profile while the GPR is scanning, so that the number of scans per unit of distance is a function of the pulse repetition and the pulling speed (which tends to vary during profiling). The result of continuous profiling is a non-uniform basic quality profile, which normally has to be spatially re-sampled. However, in stationary point collection, the antennas are fixed at the measurement point while the scans are being stacked (i.e., added and averaged), resulting in a substantial increase in the signal to noise ratio (significant improvement of GPR data can be achieved by stacking 16 – 128 times). When the operator is satisfied with the data quality, the antennas are moved at uniform intervals to the next stations along the profile, stacking each one at a time.
Extensive development and improvement in the hardware and software of the new systems, such as the RAMAC GPR used to collect the data for this thesis, have made it possible to combine the two methods to create a continuous-stationary collection mode. Operating the RAMAC GPR (see Appendix B) at a pulse repetition rate of 100 kHz, with a distance-calibrated survey wheeland a bi-directional (enhanced) parallel port for control-computer communication of 4 Mbit/s, enable collecting stacked data at point stations while continuously moving the antennas. Measurements in the Evrona (southern Arava valley, Israel) study site were taken at uniform intervals of 0.25 m between stations, while moving at an average speed of about 0.5 m/s with the antennas lifted about 5-10 cm above the surface. At each station, the GPR pulses were stacked 16-32 times for 0.25 s, resulting in each station having a linear dimension of about 0.125 m. Thus, for all practical purposes, the stations can be considered point stations.
Reflection and diffraction
When operating a GPR system in the conventional reflection mode, a reflection profile is obtained. Most of the returned signals in such a profile are reflections from subsurface discontinuities, although other types of waves may also be present. Wave types such as a direct airwave, a critically refracted airwave and a direct ground wave generally appear as well, as predicted by the Ray Theory and simple geometrical relations. In a reflection profile, the principal reflections are generally more or less immediately identifiable, as can be seen, for example, in Figures 2b and 2c. Note that most of the signals in the profiles are reflections exceptthe two topmost, which are two direct waves from the transmitter to the receiver, one in the air and the other in the ground.
In certain common conditions during GPR investigations, in addition to reflections, the EM waves undergo diffractions from small inhomogeneities and objects. Diffractions that can be identified as hyperbolas in the time section occur in two cases: when the dominant wavelength, Lc, in the radar pulse is larger than the dimensions of the diffractions’ source, and when waves are diffracted from sharp edges. The physical relation between the velocity, v, wavelength, L , and frequency, f, of an EM wave is given by the equation:
(2) v = Lf
According to relation 2, if, for example, a GPR signal were transmitted at a center frequency of 100 MHz into geological environment such as Evrona, with an average propagation velocity of 0.1 m/ns, the local dominant wavelength of the propagating signal would be approximately 1 m. Therefore, diffraction patterns would be obtained from objects or inhomogeneities that are smaller than 1 m. A clear diffraction pattern can be seen in Figures2b and 2c at a depth of 8 m under the 60 m coordinate position.
Resolution
The resolution of a GPR image is controlled by the sharpness of the focus of the system. The resolutionis defined by the Rayleigh criterion as the ability to distinguish between two close signals obtained during the GPR mapping, before their separate identity is lost and they appear to be one event. The range resolution, dl, can be practically defined as the half-wavelengthof the GPR signal in the geological medium, i.e.:
(3) dl ~ v/fc = 0.5 kc
where v is the average propagation velocity (although Widess [1973] showed that the limit of the range resolution can reach kc/8 in case of excellent data). Processing methods such as deconvolution can enhance the range resolution below a quarter of the wavelength. For example, the calculated average basic vertical resolution for a 100 MHz center frequency mapping of an alluvial environment such as Evrona is about 0.5 m (or Widess resolution of 0.125 m, see Appendix C for the basic resolution of other common geological materials).
A reflecting horizon may vary laterally in dielectric constant, thus changing the reflection coefficient, or stop laterally, as a result of faulting or absence of deposition (e.g., channel sands). Horizontal (or spatial) resolution refers to the ability to detect the lateral changes in reflectors, such as those caused by faults or facies changes. In this case, the reflected energy that arrives at the receiver antenna does not come from a single point of incidence, but from a circular zone on the reflector. If t is the two-way time of a reflection, fc the frequency of a radar wave and v the velocity, the first Fresnel zone radius Fr from which most energy comes, is:
(4) Fr ~ 0.5 v (tr/fc)1/2
The derivation of the Fresnel zone radius approximation for GPR is exactly analogous for seismic waves, although in reality, since GPR systems generally use directional dipole antennas, the EM sheaf of waves forms the shape of an elliptical cone (the long axis is perpendicular to the dipole). According to equation 4, if the area of a reflector is greater than an area bordered by circular zone with radius Fr, its shape will be accurately mapped on the time section. However, if the areal extent of the reflector is smaller, diffraction patterns from the edges may dominate its shape. From equation 4, it can be understood that that spatial resolution decreases as a function of depth (e.g., with the increase of the time).
To illustrate, in the alluvial environment of Evrona (southern Arava valley, Israel, average propagation velocity of 0.1 m/ns), the calculated spatial resolution of a reflector is about 4.5 m (2Fr) at the depth of 10 m (i.e. tr = 200 ns) achieved in the 100 MHz GPR profiles. This means that the reflector must be larger than 4.5 m, in order to be best mapped. In practice, the spatial resolution is substantially better. Sheriff [1985] discusses an effective Fresnel zone as equal to half the size of the first Fresnel zone. Therefore, it can be shown that when such a reflector occupies only 25 percent of the Fresnel zone, its reflected amplitude decreases only by 40 percent. This result emphasizes the fact that even reflectors with lateral dimensions of 1 m (about ¼ Fr)can be clearly detectable at a depth of 10 m, in conditions of fair signal to noise ratio.
Time window, velocity and depth
The time length between two transmitted pulses for which the reflections are recorded is called the time window, Tw , or the total two-way travel time, since the pulse travels to the reflectors and back. The propagation velocity of GPR waves in non-conducting and non-media is approximately c/ (K)1/2, where c is the velocity of light in vacuum (0.3 m/ns) and K is the dielectric constant (or relative permittivity). Since the dielectric constants of most dry and non-conducting rocks and soils vary within about 5-15, the propagation velocity in the ground is normally between about 0.077 and 0.134 m/ns (see AppendixA). Propagation Velocity measurements of geological environments can be done by GPR through CMP(common mid-point) or WARR (wide-Angle reflection-refraction) sounding methods. Transillumination mode is efficient for measuring velocities inside accessible rock bodies such as tunnels and quarries, or objects such as pillars, walls, bridges, etc. Another simple approach to determining the velocity of a radar pulse in the ground using the conventional reflection mode is to locate a surface outcrop of rock or some buried reflecting object whose depth is known and measure the two-way time for the reflection from it.
When converted to depth, the time window limits the maximum depth (or maximum range) of acquisition in the GPR profile (presuming sufficient penetration of the EM waves). For a short transmitter-receiver offset relative to the total depth, the profile depth, D, can be calculated as half of the time window, Tw, multiplied by the average propagation velocity, v,of the pulse inside the geological media (i.e., D ~ 0.5 Tw v). Otherwise, it can be shown from simple geometrical relations that for a transmitter-receiver offset,x, the precise depth to a reflector, d, located at two-way time, t, is given by the equation:
(5) d = 0.5 (v2t2+x2)1/2
Appendix A
Electrical Properties of Geological Media Material Dielectric constant Conductivity (mS/m) Velocity (m/ns) Attenuation (dB/m)
| Material | Dielectric constant | Conductivity (mS/m) | Velocity (m/ns) | Attenuation (dB/m) |
| Air | 1 | 0 | 0.3 | 0 |
| Distilled water | 80 | 0.01 | 0.033 | 0.002 |
| Fresh water | 80 | 0.5 | 0.033 | 0.1 |
| Sea water | 80 | 30,000 | 0.01 | 1,000 |
| Dry sand | 3-5 | 0.01 | 0.15 | 0.01 |
| Saturated sand | 20-30 | 0.1-1.0 | 0.06 | 0.03-0.3 |
| Limestone | 4-8 | 0.5-2 | 0.12 | 0.4-1 |
| Shale | 5-15 | 1-100 | 0.09 | 1-100 |
| Silt | 5-30 | 1-100 | 0.07 | 1-100 |
| Clay | 4-40 | 2-1,000 | 0.06 | 1-300 |
| Granite | 4-6 | 0.01-1 | 0.13 | 0.01-1 |
| Salt (dry) | 5-6 | 0.01-1 | 0.13 | 0.01-1 |
| Ice | 3-4 | 0.01 | 0.16 | 0.01 |
Table A.A: Electrical properties of geological media [after Davis et al., 1989]
Appendix B
RAMAC GPR – Technical Specifications
Manufacturer
Radar unit
A/D Converter: 16 bit
Pulse Repetition Frequency: 100 kHz
Scan Rate: up to 200 scans/sec
Performance Factor: 150 dB
Time Window: up to 6 µsec
Number of samples/trace: 128 – 2048
Number of stacks: 1 – 32768
Sampling frequency: 0.4 -100 GHz
Data Transfer Rate: 4 Mbit/sec
Operating Temperature: -10? C – +50? C
Humidity: 0 – 100% (RH)
Trig functions: Distance Pulse Encoders, Time, Keyboard or External
Communication: Serial, Normal or Enhanced Parallel ports to a PC computer.
Optical Fibers (4-300 m) between the Transmitter, Control and Receiver
Input Voltage: 6 – 14 VDC
Weights
Control unit with battery: 4.9 kg
Transmitter/Receiver 2.4 kg
(with 200 MHz antenna and batteries)
Antennas
10, 25, 50, 100, 200, 400 MHz, unshielded
200, 500, 1000 MHz, shielded
100, 250 MHz borehole, 48 mm OD
Appendix C
Computed Values of Vertical Resolution [cm] of GPR Waves Inside Geological Media Material Dielectric constant Vertical Resolution (cm)
| Material | Dielectric constant | Vertical Resolution (cm) | ||
| fc= 100 MHz | fc= 200 MHz | fc= 500 MHz | ||
| Air | 1 | 150 | 75 | 30 |
| Distilled water | 80 | 17 | 8.5 | 3.5 |
| Fresh water | 80 | 17 | 8.5 | 3.5 |
| Sea water | 80 | 17 | 8.5 | 3.5 |
| Dry sand | 3-5 | 87-67 | 43.5-33.5 | 17.5-13.5 |
| Saturated sand | 20-30 | 34-27 | 17-13.5 | 7-5.5 |
| Limestone | 4-8 | 75-53 | 37.5-26.5 | 15-10.5 |
| Shale | 5-15 | 67-39 | 33.5-19.5 | 13.5-9.5 |
| Silt | 5-30 | 67-27 | 33.5-13.5 | 13.5-5.5 |
| Clay | 4-40 | 67-24 | 33.5-12 | 13.5-5 |
| Granite | 4-6 | 75-61 | 37.5-30.5 | 15-12 |
| Salt (dry) | 5-6 | 67-61 | 33.5-30.5 | 13.5-12 |
| Ice | 3-4 | 87-65 | 43.5-37.5 | 17.5-13 |
Table A.C: Vertical resolution of GPR wave [after Basson, 1992]
These values, which are half-wavelengths of the propagating signals inside the geologic media, represent a practical resolution. In the case of very good signal to noise ratio, the theoretical resolution can be increased up to a one eighth of the wavelengths [Widess, 1973], i.e., quarter of the presented values.
References
Annan, A. P., and Davis, J. L., 1977. Impulse radar applied to ice thickness measurements and freshwater bathymetry. Geological Survey of Canada, Report of activities, Paper 77-1B, pp. 117-124.
Basson U., 1992. Mapping of moisture content and structure of unsaturated sand layers with ground penetrating radar. Thesis submitted for the degree of master of Sciences in Geophysics, October 1992, Tel-Aviv University, Raymond and Beverly Sackler, Faculty of Exact Sciences, Department of Geophysics and Planetary Sciences, 80 p. (in Hebrew with English abstract).
Basson, U., 2000. Imaging of active fault zone in the Dead Sea Rift: Evrona Fault Zone as a case study. Thesis submitted for the degree of Ph.D., Tel-Aviv University, Raymond & Beverly Sackler, Faculty of Exact Sciences, Department of Geophysics & Planetary Sciences, 196 p.
Cook, J.C., 1995. Preface, Journal of applied Geophysics, Vol. 33, p. 1-3.
Davis, J. L., and Annan, A. P., 1986. High resolution sounding using ground probing radar. Geoscience Canada, Vol. 13(3), p. 205-208.
Davis, J. L., and Annan, A. P., 1989. Ground penetrating radar for high resolution mapping of soil and rock stratigraphy. Geophysical prospecting, Vol. 37, p. 531-551.
Dobrin, B. M. and Savit, C. H., 1988. Introduction to Geophysical Prospecting. International Edition, McGraw-Hill Book Co.
Morey, R.M., 1974. Detecting of subsurface cavities by ground penetrating radar. Highway Geological symposium, Proceedings 27, p. 28-30.
Parasnis, D. S., 1997. Principles of Applied Geophysics (fifth edition). Chapman & Hall.
Ulriksen, C. P. F., 1982. Applications of impulse radar to civil engineering. Unpublished Ph.D. thesis, Department of Engineering Geology, Lund University of Technology, Sweden. (Republished by Geophysical Survey Systems Inc., Hudson, New Hampshire).
Widess, M. B., 1973. How thin is this bed? Geophysics, Vpl. 38, p. 176-1180.
Yilmaz, O., 1987. Seismic Data Processing.Edited by Doherty S., M., Society of Exploration Geophysics, Series: Investigation in Geophysics, Vol. 2.


